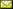Spectral deferred correction methods for second-order problems
Working Groups: Lehrstuhl Computational Mathematics
Collaborators (MAT): Ikrom Akramov, M. Sc., Prof. Dr. Daniel Ruprecht, Dr. Sebastian Götschel
Collaborators (External): Michael Minion, Robert Speck
Description
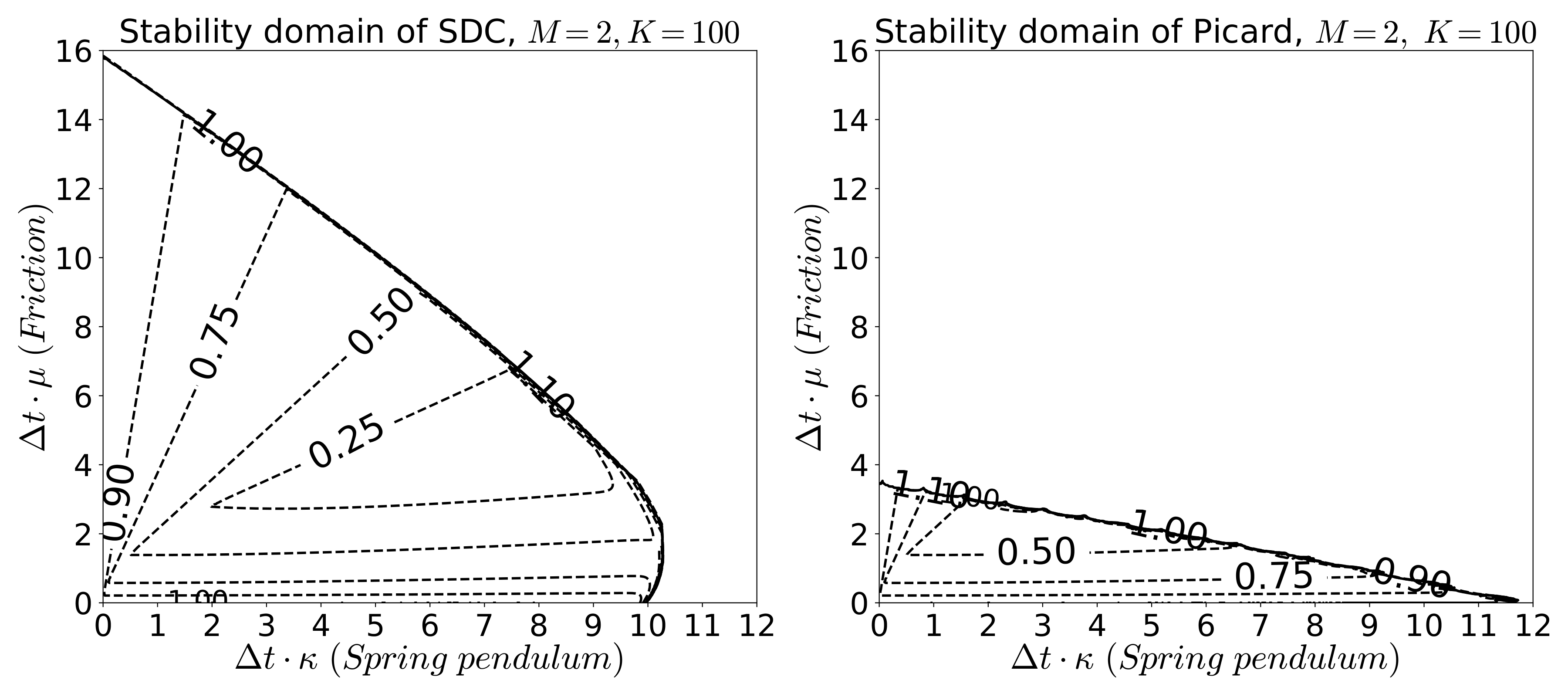
Spectral deferred correction (SDC) methods are iterative schemes for computing the numerical solution of initial value problems. We focus on applying SDC to second-order ordinary and partial differential equations. There is a version of second-order SDC called Boris-SDC [1] and it is used in plasma physics and also in computing fast ion trajectories in nuclear fusion reactors [2]. The main advantages of SDC methods are that they can reach any order of convergence and also cover a large stability domain. We are using SDC method to find the numerical solution to the second-order ODEs by analyzing the convergence and stability of the method. In the image below, one can compare the stability region of the SDC iteration and Picard iteration for the damped harmonic oscillator problem. This picture shows that the stability region of the SDC method is much larger than the corresponding region by the Picard method.