Research Topic: Size-Ramsey Numbers
Collaborators (MAT): Dr. Dennis Clemens, Prof. Dr. Anusch Taraz
Collaborators (external): Barnaby Roberts, Guilherme Oliveira Mota, Mathias Schacht, Matthew Jenssen, Meysam Miralaei, Natasha Morrison, Yoshiharu Kohayakawa, Damian Reding
Given any graph \(H\), a natural question to ask is how large a Ramsey graph for \(H\) needs to be in terms of the number of edges. This leads to the definition of the size-Ramsey number \(\hat{r}(H)\), introduced in [EFRS1978], which is the smallest number of edges among all Ramsey graphs for \(H\).
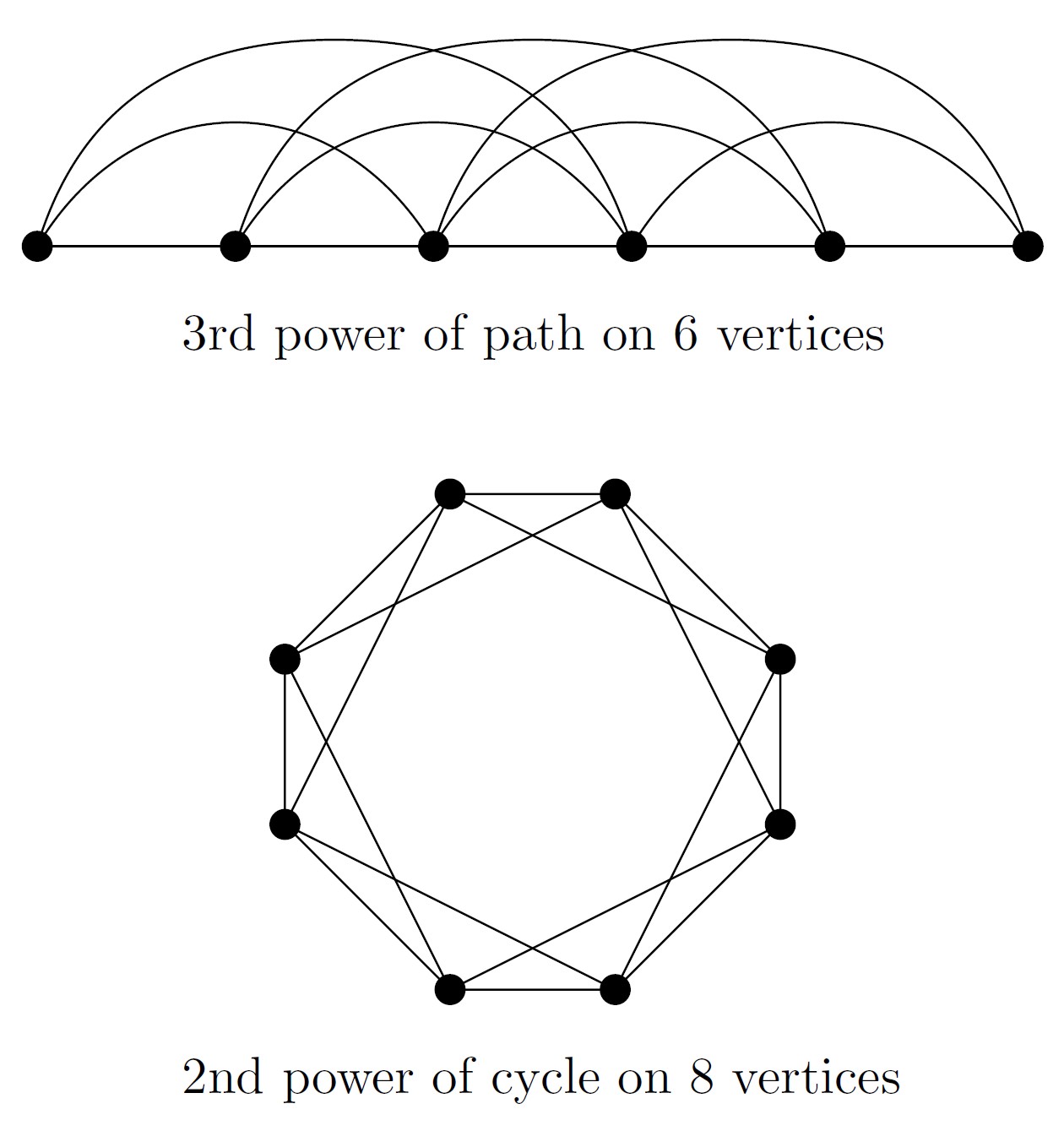
Addressing a question posed by Erdős [Er1981], Beck [Be1983] proved that the size-Ramsey number of the path \(P_n\) on \(n\) vertices is linear in \(n\). That is, there exists a constant \(C>0\) such that \(\hat{r}(P_n)<Cn\) for all positive integers \(n\). We generalized this further by showing that powers of paths and cycles also have a linearly growing size-Ramsey number [CJKMMRR2019], which was extended even further in [BKMMMMP2019], [HJKMR2020], [KLWY2021].
Moreover, Rödl and Szemerédi [RS2000] conjectured that for every integer \(\Delta \geq 3\) there exists a positive real \(\varepsilon = \varepsilon(\Delta)\) such that \[ n^{1+\varepsilon} \leq \max \hat{r}(H) \leq n^{2-\varepsilon} \] for every large enough \(n\), where the maximum is taken over all \(H\) on \(n\) vertices and with maximum degree at most \(\Delta\). The upper bound of this conjecture was confirmed by Kohayakawa, Rödl, Schacht, and Szemerédi [KRSS2011], but the lower bound remains an open problem. A natural candidate for proving the lower bound could be the grid \(G_{\lfloor \sqrt{n} \rfloor,\lfloor \sqrt{n} \rfloor}\) on (roughly) \(n\) vertices. While it is still unknown whether the grid supports the mentioned lower bound, we [CMRST2021] were able prove the currently best known upper bound on \(\hat{r}(G_{\lfloor \sqrt{n} \rfloor,\lfloor \sqrt{n} \rfloor})\), giving that
\[ \hat{r}(G_{\lfloor \sqrt{n} \rfloor,\lfloor \sqrt{n} \rfloor}) = O\left( n^{\frac{3}{2}+o(1)} \right)\, . \]
References
[Er1981] P. Erdős, On the combinatorial problems which I would most like to see solved, Combinatorica 1 (1), 25–42, 1981.
[EFRS1978] P. Erdős, R. J. Faudree, C. C. Rousseau, and R. H. Schelp, The size Ramsey number, Periodica Mathematica Hungarica 9 (1-2), 145–161, 1978.