Research Area: Ramsey Theory
Working Groups: Lehrstuhl Diskrete Mathematik
The fundamental principle of Ramsey theory can be described as follows: every large enough mathematical object, e.g. a complex network, contains a well-structured sub-object. While such principle can be observed in many branches of mathematics, Ramsey-type results from Combinatorics and Graph Theory have been applied in and stimulated research on many other fields of Mathematics, including Number Theory and the Probabilistic Method.
In Graph Ramsey Theory the above principle is usually presented through the discussion of edge colourings: given any two graphs \(H\) and \(G\), we say that \(G\) is a Ramsey graph for \(H\), denoted by \(G\rightarrow H\), if every colouring of the edges of \(G\) with only two colours leads to a monochromatic subgraph of \(G\) which is isomorphic to \(H\). The fundamental result of Ramsey [Ra1930] then states that for every \(H\) there exists a graph \(G\) such that \(G\rightarrow H\) holds. For instance, denote with \(K_n\) a complete graph on \(n\) vertices, then it is an easy exercise to show that \(K_6\rightarrow K_3\).
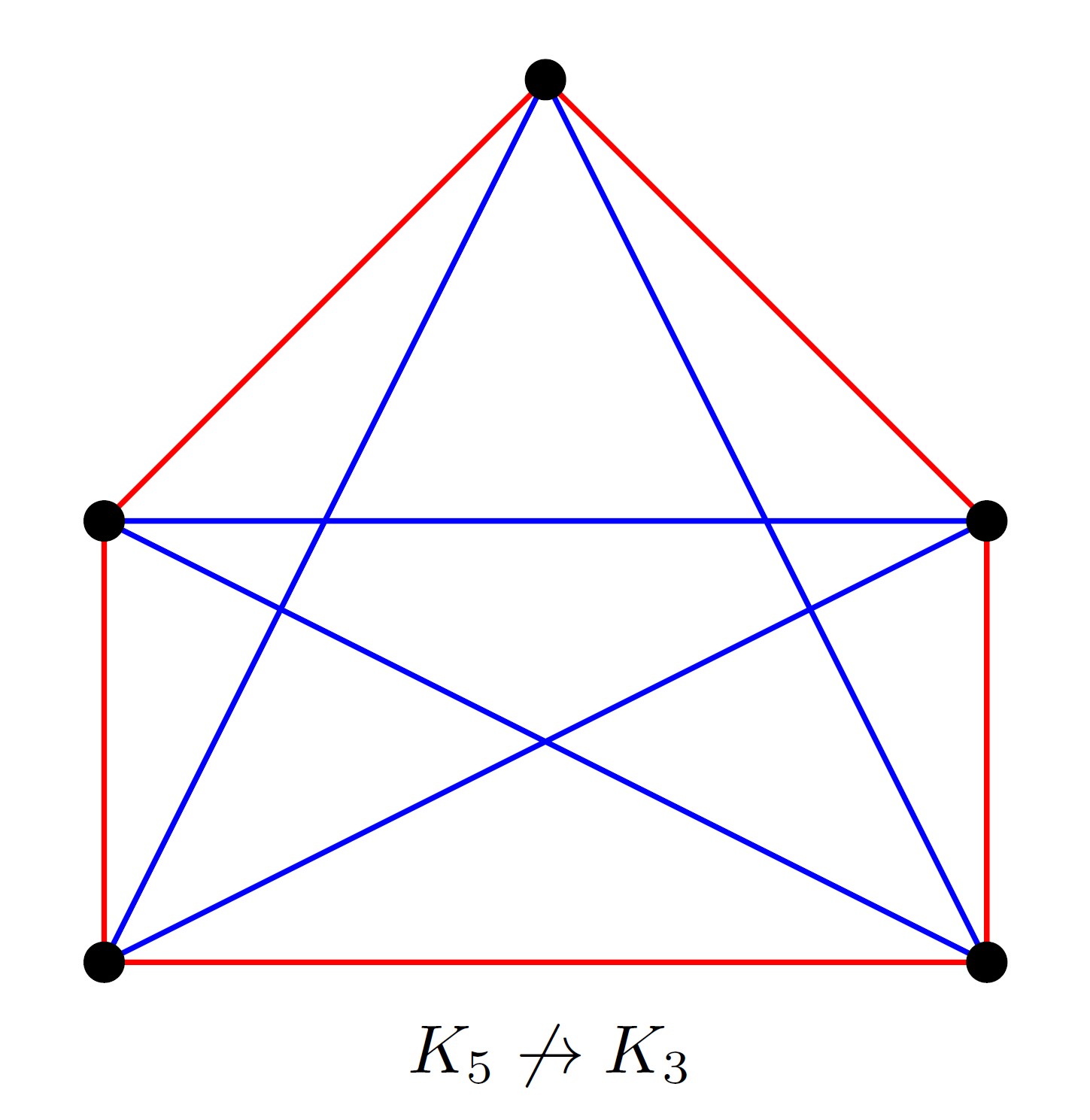
Obviously, a natural question to ask is how many vertices a graph needs in order to be Ramsey for another graph \(H\). This leads to the famous Ramsey number \(r(H)\), which turns out to be incredibely hard to determine even for the case when \(H=K_5\). Indeed, for general \(n\), the best known bounds on \(r(K_n)\) are of the form
\[2^{\left(\frac{1}{2}+o(1)\right)n} \leq r(K_n) \leq 2^{\left(2-o(1)\right)n}\]
first obtained by Erdős [Er1947] and by Erdős and Szekeres [ES1935] more than 70 years ago, with further improvements only in the \(o(1)\)-terms by Spencer [Sp1975], Conlon [Co2009] and Sah [Sa2020].
However, despite the search for precise or at least asymptotic results on Ramsey numbers, research in Graph Ramsey Theory developed many different directions leading to many interesting and challenging research topics. For recent developements on Graph Ramsey Theory, see e.g. [CFS2015]. Nowadays, one of the central aims is to understand structural properties (e.g. sizes of graph parameters) of Ramsey graphs, to classify given graphs by their Ramsey behaviour or to study the Ramsey behaviour of random graphs.
Literature
[Co2009] D. Conlon, A new upper bound for diagonal Ramsey numbers, Annals of Mathematics, 941–960, 2009.
[CFS2015] D. Conlon, J. Fox, and B. Sudakov, Recent developments in graph Ramsey theory, Surveys in Combinatorics 424, 49–118, 2015.
[ES1935] P. Erdős and G. Szekeres, A combinatorial problem in geometry, Compositio Mathematica 2, 463–470, 1935.
[Sa2020] A. Sah, Diagonal Ramsey via effective quasirandomness, arXiv preprint arXiv:2005.09251, 2020.