From the mathematical point of view, PBEs are nonlinear, nonlocal transport equations which allow a balancing of the number concentration w.r.t. intern variables (e.g. length, diameter) over time. For real process chains the whole system has to be represented mathematically. The general form involves the following nonlinear partial differential equation with given initial and boundary data

$$\begin{align*}
    \dot{q}(x,t)+\partial_x\big(R[W[q,\gamma,a,b]](x,t)q(x,t)\big) &= h[q](x,t) && t>0,x\in[x_{\min},\infty)\\
    q(x_{\min},t) & = n(t)\\
    q(x,0) & = q_0(x)\\
    W[q,\gamma,a,b]&= \int\limits_{a(x)}^{b(x)}\gamma(t,x,y)q(y,t)\text{d} y.
\end{align*}$$

In the context of a mathematical analysis of the upper equations, the already existing theory regarding nonlocal transport equations was problem-specifically extended such that also nonlocalities in the source terms (e.g. feedback by mills and screens within a spray granulation process chain) as well as ripening velocities depending nonlocally on the disperse properties (e.g. total surface, total mass in the particle size distribution) can be considered. Via the method of characteristics and fixed-point arguments it was possible in a joint work with Dr. A. Keimer (EECS, Berkeley) to set up conditions which guarantee the existence of a unique and sufficiently regular solution.

Based on the mentioned analysis, a numerical method was realized which could be applied, among others, on the study of spray granulation processes. For this numerical implementation the nonlocal partial differential equation was transformed to a nonlinear system of ordinary differential equations by use of the method of characteristics and by discretizing the disperse properties. This transformation facilitates the construction of an efficient numerical method by using a time-discretization scheme as well as an adaptive discretization in the spatial and time variable.

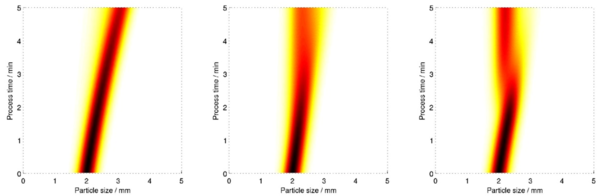
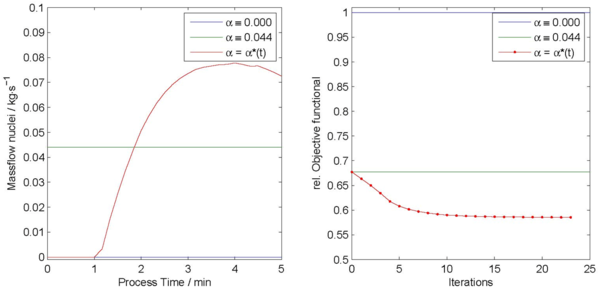
In view of the calculation of sensitivities, it was possible not only to simulate the given process but also to simulate and to verify the adjoint PBE after prescribing an objective functional. Thereby, within this subproject C5 the derivation of the adjoint equation occured by applying the so-called Lagrange formalism w.r.t. time-dependent control parameters. The implemented first order optimization method based on the previous procedure was exemplarily, in cooperation with the working group Heinrich (A3,Z), applied on a PBE which models a spray granulation process coupled with a filtered and milled feedback. Thereby, the time-dependent parameter to control corresponds to the inflow rate of new nuclei. As you can see in fig. 1, you can goal-orientedly influence the dynamic process by controlling the mass flow. Moreover, as illustrated in fig. 2, the mass to be milled can be reduced by choosing an optimal constant control. Furthermore, an iterative calculation of a time-dependent locally optimal control shows that the previous mentioned mass can be diminished even more. This mass reduction evidently decreases the energy you have to spend for it.

Within the scope of a simulation and optimization of micro reaction plants considerd within the DFG priority program, the simulation tool FIMOR (Fully Implict Method for Ostwald Ripening), which was developed in our research group, was exploited in order to perform in subproject A8 (working group Peukert) model-based parameter studies w.r.t. the different control parameters. Due to the efficient implicit implementation and the low number of control variables, it was possible to establish within a cooperation of working group Peukert and working group Leugering optimal process conditions for the desired product attributes respectively without using gradient information. Moreover, some model-based optimization results could be realized on a micro reaction plant considered within subproject A8.