Bei PBEs handelt es sich aus mathematischer Sicht um nichtlineare, nichtlokale Transportgleichungen, welche die Anzahlkonzentration bezüglich interner Variablen (z.B. Länge, Durchmesser) über die Zeit bilanzieren. Für reale Prozessketten muss das ganze System mathematisch abgebildet werden. In allgemeiner Form handelt es sich um die folgende nichtlineare partielle Differentialgleichung mit gegebenen Anfangs- und Randdaten:

$$\begin{align}
    \dot{q}(x,t)+\partial_x\big(R[W[q,\gamma,a,b]](x,t)q(x,t)\big) &= h[q](x,t) && t>0,x\in[x_{\min},\infty)\\
    q(x_{\min},t) & = n(t)\\
    q(x,0) & = q_0(x)\\
    W[q,\gamma,a,b]&= \int\limits_{a(x)}^{b(x)}\gamma(t,x,y)q(y,t)\text{d} y.
\end{align}$$

Im Rahmen der mathematischen Analyse der Gleichungen wurde die existierende Theorie zu nichtlokalen Transportgleichungen problemspezifisch erweitert im Hinblick auf auftretende nichtlokale Quellterme (z.B. Rückführung durch Mühle und Siebe innerhalb einer Sprühgranulations-Prozesskette) sowie auf nichtlokal von den dispersen Eigenschaften abhängenden Reifungsgeschwindigkeiten (z.B. gesamte Oberfläche, Gesamtmasse in der Partikelgrößenverteilung). Mittels der Methode der Charakteristiken und Fixpunktargumenten konnten in Kooperation mit Dr. A. Keimer (EECS, Berkeley) Voraussetzungen aufgestellt werden, um die Existenz einer eindeutigen Lösung mit hinreichender Regularität zu garantieren.

Auf der obigen Analyse basierend wurde ein numerisches Verfahren realisiert, das unter anderem auch auf die Untersuchung von Sprühgranulationsverfahren angewendet werden kann. Für dieses numerische Verfahren wurde mittels der Methode der Charakteristiken die nichtlokale partielle Differentialgleichung durch eine Diskretisierung der dispersen Eigenschaften in ein nichtlineares System gewöhnlicher Differentialgleichungen transformiert. Auf dieser Transformation basierend wurde mittels eines Zeitintegrationsschemas sowie adaptiver Orts- und Zeit-Diskretisierung ein effizientes Verfahren konstruiert.

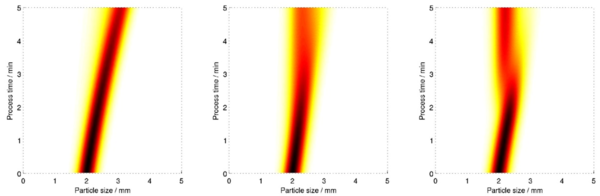
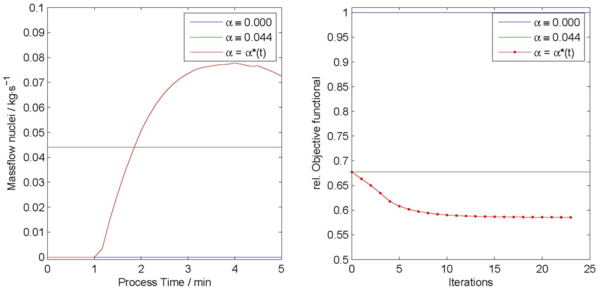
Im Hinblick auf die Sensitivitäten wurde damit neben der Simulation des Prozesses bei Vorgabe eines Zielfunktionals auch die adjungierte Populationsbilanzgleichung simuliert und verifiziert. Dabei wurde diese innerhalb des Teilprojekts C5 über den sogenannten Lagrange-Formalismus im Bezug auf zeitabhängige Steuerungsgrößen hergeleitet. Das darauf aufbauend implementierte Optimierungsverfahren erster Ordnung wurde in Kooperation mit AG Heinrich (A3,Z) exemplarisch an einer PBE angewandt, welche die Sprühgranulation gekoppelt an eine gefilterte und gemahlene Rückführung modelliert. Die zu steuernde zeitabhängige Größe entspricht der Zuflussrate an neuen Keim-Partikeln. Wie in Abb. 1 zu sehen ist, lässt sich durch die Steuerung dieses Massenstroms der dynamisch ablaufende Prozess zielorientiert beeinflussen. Wie in Abb. 2 dargestellt ist, kann die zu mahlende Masse durch die Wahl einer optimalen konstanten Steuerung reduziert werden. Des Weiteren kann durch die iterative Berechnung einer zeitabhängigen lokal optimalen Steuerung diese zu mahlende Masse weiter reduziert werden. Durch die Reduktion dieser Masse wird natürlich auch die dafür aufzubringende Energie verringert.

Im Rahmen der Simulation und Optimierung von Mikroreaktionsanlagen im Rahmen des SPPs wurde das in unserer Gruppe entwickelte Simulationstool FIMOR (Fully Implict Method for Ostwald Ripening) genutzt, um in Teilprojekt A8 (AG Peukert) Parameterstudien der verschiedenen Steuergrößen modellbasiert durchzuführen. Aufgrund der effizienten impliziten Implementierung und der geringen Anzahl an Steuergrößen konnten dadurch innerhalb einer Kooperation von AG Peukert und AG Leugering optimale Prozessbedingungen für die jeweils gewünschten Produkteigenschaften gradientenfrei bestimmt werden. Zudem konnten einige modellbasierte Optimierungsresultate innerhalb von Teilprojekt A8 an einer Mikroreaktionsanlage umgesetzt werden.