Morphologische Modellierung und Simulation von Kristallisatisationsprozessen
- Institut:
Wissenschaftszentrum Weihenstephan für Ernährung, Landnutzung und Umwelt, Lehrstuhl für Systemverfahrenstechnik, TU München
- Projektleiter:
Dr.-Ing. Prof. Dr.-Ing. habil. H. Briesen, TU München
- Bearbeiter:
Projektziel
Die Partikelform ist eine wichtige Eigenschaft, die sowohl die Verarbeitung von Partikeln als auch deren physikalische Eigenschaften stark beeinflusst. Kristalle werden klassischerweise als konvexe Polyeder betrachtet und deren Form durch die Flächenabstände zum Polyedermittelpunkt beschrieben. Da ein solcher Kristall mehrere verschiedene Flächen hat, führt das in der Prozessmodellierung auf hochdimensionale Populationsbilanzmodelle, die einen hohen Rechenaufwand während der Simulation erfordern. Aus diesem Grund werden in der aktuellen Praxis oft Formfaktoren definiert, die die Partikelform allerdings nicht eindeutig beschreiben aber die Dimension der Populationsbilanzgleichung hinreichend reduzieren. Weiterhin, muss die Partikelform experimentell charakterisiert werden, um Simulationsergebnisse zu validieren und neue Erkenntnisse über den Prozess zu erhalten. Üblicherweise versucht man hierzu aus Mikroskopbildern die Information über der Partikelform- und Größenverteilung der Kristallpopulation zu gewinnen. Die Anwendung solcher Verfahren ist aber eingeschränkt, da es durch die 2D Projektion des Kristalls im Mikroskopbild immer zu Informationsverlusten kommt. Eine weitere Herausförderung ist es, nicht nur facettierte Einzelkristalle, sondern auch die abgerundete und aggregierte Partikel bezüglich deren Form sowohl experimentell als auch modelltechnisch zu beschreiben.
Das Ziel dieses Projektes ist es, Simulations- und Partikelcharakterisierungsverfahren zu entwickeln, um Partikelform umfassend zu beschreiben. Die Partikel werden experimentell durch Messungen mit einem Mikrocomputertomographen charakterisiert. Dieses Messverfahren hat sich vor allem in den Materialwissenschaften etabliert, da es die nicht-destruktive Rekonstruktion der vollen 3D Struktur ermöglicht.
Ergebnisse der 1.-2. Förderperiode

Experimentelle Charakterisierung
Durch Mikrocomputertomographie erhaltene Bilder ermöglichen die volle 3D Beschreibung der Kristallform. Der entwickelte Bildverarbeitungsalgorithmus identifiziert die Flächen und Flächenabstände anhand gegebenen Formmodels [1].
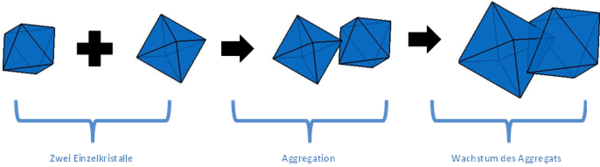
Außerdem ist es möglich, Kristallaggregate in Primärpartikel zu zerlegen und die Orientierung der Primärpartikel in einem Aggregat zu messen [4]. Die Messung der Primärpartikelorientierung kann zu einem besseren Verständnis des Aggregationsprozesses führen [7].
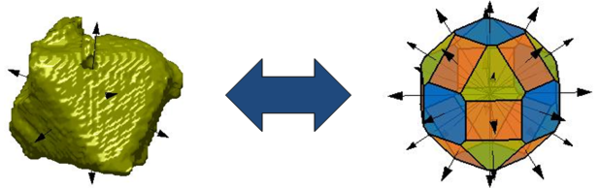

Üblicherweise wird die Partikelform durch die Flächennormalen und die Distanz jeder Fläche vom Mittelpunkt definiert. Die Populationsbilanzgleichung für reine Wachstumsprozesse beschreibt die zeitliche Entwicklung der Partikelgröße und –form:
$$ \frac{\delta n}{\delta t}+\sum_i{\frac{\delta\left( g_i, n\right)}{\delta h_t}}=0 $$
Dabei sind die flächenspezifischen Wachstumsraten von der Übersättigung abhängig. Zur Schließung der Massenbilanz muss das Volumen der Kristalle berechnet werden:
$$ I_{volume}=\int{\mu_{volume}\left(h_C\right) n\left(h_C\right)d h_C} $$
Allerdings steigt auch hier die Dimension des Problems mit der zu berücksichtigenden geometrischen Komplexität der Kristalle. Dieses vorwiegend numerische Problem wurde gelöst durch eine Kombination von Charakteristikenverfahren und Monte Carlo Integration [3].
Für Aggregationsprozesse ist es nicht möglich, die volle Form der wachsenden Kristallaggregate in einem Kristallisationsprozess durch eine solche deterministische Populationsbilanzgleichung zu beschreiben. Die üblichen Ansätze lösen dieses Problem durch der Annahme dass zwei Körper nach der Aggregation einen neuen, Volumen-äquivalenten Körper bilden. Allerdings hat der Volumen-äquivalente Körper immer eine zu kleine Fläche. Alternativ können Monte Carlo Simulationen durchgeführt werden, wobei jedes Partikel in einem kleinem Volumenausschnitt des Systems einzeln simuliert wird. Nur durch solche Simulationen lässt sich die Kristallfläche richtig abbilden und die dazugehörige Massenbilanz richtig schließen [6].
Alternativ zu den obengenannten Formbeschreibungen, lässt sich in der Konvexgeometrie die Minkowski-Addition verwenden, um den konvexen Körper $B$ als Summe sogenannter strukturierenden Elemente $S_iS zu betrachten:
$$B=\sum_i{\lambda_i S_i} $$
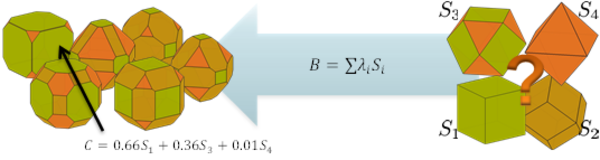
Der theoretische Hintergrund war Grundlage für diese Projekt. Ein großer Vorteil einer solchen Charakterisierung ist die Möglichkeit abgerundete Partikel zu beschreiben:
Kombiniert mit den entsprechenden Bildverarbeitungsschritten ermöglicht dieses Verfahren eine Beschreibung des Partikelabriebs [2].

Arbeitsprogramm für die 3. Förderperiode
Monte Carlo Simulationen von Kristallaggregation und Kristallwachstum ermöglichen es, die Form der Kristallaggregate und die entsprechende Flächenänderung richtig zu ermitteln. Allerdings sind solche Simulationen rechenaufwendig und eignen sich daher nicht für Prozessregelung, Optimierung oder große Parameterstudien. Außerdem lassen sie sich nur schwer mit anderen Prozessschritten die eine einfachere Formbeschreibung verwenden zusammenführen. Ziel ist es beide Methoden zu vereinigen. Dazu wird die zeitliche Entwicklung der Fläche einzelner Aggregate erfasst und eine Wachstumsrate aus mehreren solchen Simulationen ermittelt. Diese Wachstumsrate wird dann in einer Populationsbilanz verwendet, die Kristallwachstum und Aggregation betrachtet, wobei sowohl das Volumen $V$ als auch die Fläche $A$ der Partikel bei Aggregation erhalten bleiben:
$$\begin{align}
\frac{\delta f}{\delta t} + \frac{\delta \left(G_V f\right)}{\delta_V} & + \frac{\delta \left(G_A f\right)}{\delta_A} = \\
& \frac{1}{2}\int_{V=0}^V \int_{A=0}^{A} {\beta \left(V', V-V', A', A-A'\right) f\left(V-V', A-A'\right) f\left(V',A'\right))dV' dA'} \\
& - f\left(V,A\right)\int_{V=0}^\infty \int_{A=0}^{\infty} {\beta \left(V', V, A', A\right)f\left(V',A'\right)dV' dA}\end{align}$$
Dabei ist $f$ die Partikelgrößenverteilung über Volumen und Fläche, $G_V=A G_h$ ist die Volumenwachstumsrate, die auf der Flächenwachstumsrate $G_h$ basiert und $\beta$ der Aggregationskern. Eine Validierung wird durch Vergleich mit vollen Monte Carlo Simulationen des ganzen Prozesses durchgeführt.
Die in den früheren Projektphasen entwickelten Bildverarbeitungsalgorithmen haben bislang auf die Machbarkeit für ausgewählte Kristallgeometrien fokussiert. Zur verallgemeinerten Anwendbarkeit sollen die Algorithmen auf weitere (siehe Bild) Grundformen von Kristallen erweitert und angepasst werden.