Morphological Modeling and Simulation of Crystallization Processes
- Institute:
Wissenschaftszentrum Weihenstephan für Ernährung, Landnutzung und Umwelt, Lehrstuhl für Systemverfahrenstechnik, TU München
- Project leader:
Dr.-Ing. Prof. Dr.-Ing. habil. H. Briesen, TU München
- Researcher:
Project Goal
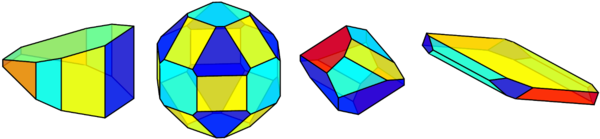
Particle shape is an important property that has a great influence on both downstream processing and the physical properties of the particulate product. Crystals are usually regarded as convex polyhedra and their shape is described by face distances from the center of the polyhedron. When modeling crystallization processes, the fact that a crystal can have several distinguished crystallographic faces leads to highly dimensional population balance models and therefore high computational effort in simulations. In current practice, this problem is often resolved by defining shape factors that, however, do not completely describe the actual shape but lead to a sufficient dimensional reduction of the population balance equation. Furthermore, the particle shape must be experimentally characterized in order to validate the simulations and gain further process insight. To this end, the information about particle shape- and size distribution is typically extracted from 2D microscopy images. However, the applicability of these methods is restricted as the 2D projection of the crystal in such an image leads to an inevitable loss of information. A further challenge is to describe not only the faceted single crystals but rounded and aggregated particles, both in terms of modeling and experimental characterization.
The goal of this project is to develop a simulation and characterization framework that fully and unambiguously describes particle shape. Particles will be experimentally characterized by microcomputed tomography measurements. This technique was established in material science, as it represents a non-destructive method for gaining information about the full 3D structure.
Results from the First Two Funding Periods

Experimental Characterization
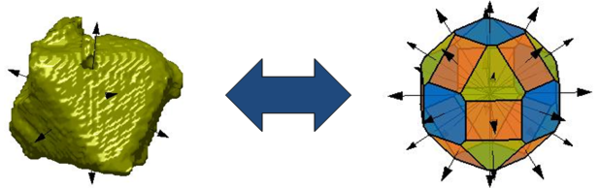
Microcomputed tomography images enable the full 3D description of particle shape. The developed image processing algorithm identifies the faces and face distances based on the given shape model [1].
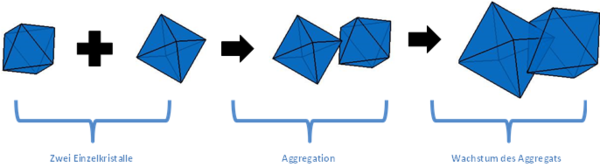
It is furthermore possible to split a crystal aggregate in primary particles and measure the orientation between the primary particles [4]. This can lead to a better understanding of the aggregation process [7].

Particle Shape and the Simulation of Crystallization Processes
Particle shape is typically described by face normals and the distances $h_i$ of each face from the center of the crystal. The population balance equation tracks the temporal development of the particle size and shape:
$$ \frac{\delta n}{\delta t}+\sum_i{\frac{\delta\left( g_i, n\right)}{\delta h_t}}=0 $$
The face-specific growth rates are supersaturation dependent. In order to close the mass balance, the total crystal volume must be computed:
$$ I_{volume}=\int{\mu_{volume}\left(h_C\right) n\left(h_C\right)d h_C} $$
The computational complexity of the problem increases with the increase of the crystals’ geometrical complexity. The resulting numerical problem was solved by a combination of the method of characteristics and Monte Carlo integration [3].
For aggregation processes, it is infeasible to fully describe the shape of growing crystal aggregates during a crystallization process by such a deterministic population balance equation. The usual approach to solving this problem is to assume that two crystals form a body of equivalent volume upon aggregation. However, the area of the volume-equivalent body is always too small. This can alternatively be solved by using Monte Carlo simulations where each particle in a small representative volume is simulated. Only these types of simulations lead to the correct computation of particle area and therefore the correct mass balance [6].
Alternatively to the shape representations described above, one can use convex geometry to describe a convex body $B$ as a weighted sum of structuring elements $S_iS :
$$B=\sum_i{\lambda_i S_i} $$
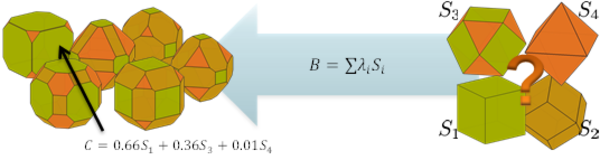
The theoretical background was the foundation of this project. One major advantage of such shape representation is the possibility of describing rounded particles.
Combined with suitable image processing steps, this method has been used for describing particle attrition [2].

Work program for the Third Funding Period
Monte Carlo simulations of crystal aggregation and growth enable the correct description of the aggregate shape and the resulting evolution of surface area over time. However, such simulations are computationally intensive and therefore not suited for process control, optimization and large parameter studies. Furthermore, they cannot be easily coupled with other process steps that use a simpler shape description. The goal is to combine these methods with a less computationally expensive classical population balance approach. To this end, the temporal evolution of the area of single aggregates will be determined from several simulations. This area growth rate $G_A$ will then be used in a population balance model of crystal growth and aggregation that preserves both the volume $V$ V and the area $A$ upon aggregation:
$$\begin{align}
\frac{\delta f}{\delta t} + \frac{\delta \left(G_V f\right)}{\delta_V} & + \frac{\delta \left(G_A f\right)}{\delta_A} = \\
& \frac{1}{2}\int_{V=0}^V \int_{A=0}^{A} {\beta \left(V', V-V', A', A-A'\right) f\left(V-V', A-A'\right) f\left(V',A'\right))dV' dA'} \\
& - f\left(V,A\right)\int_{V=0}^\infty \int_{A=0}^{\infty} {\beta \left(V', V, A', A\right)f\left(V',A'\right)dV' dA}\end{align}$$
Here, $f$ is the particle size distribution over the volume and area, $G_V=A G_h$ is the volumetric growth rate based on the face-specific growth rate $G_h$ and $\beta$ the aggregation kernel. The validation will be performed through comparison with full Monte Carlo simulations.
The image processing algorithms developed in the previous project stages were focused on the proof of concept for the chosen crystal geometries. For a generalized applicability, the algorithms will be expanded and adjusted for further crystal morphologies (see Image).